Advertisements
Advertisements
प्रश्न
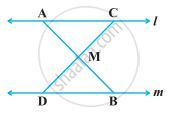
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
उत्तर
Given: In the following figure, l || m and M is the mid-point of a line segment AB i.e., AM = BM.
To show: MC = MD
Proof: l || m ...[Given]
∠BAC = ∠ABD ...[Alternate interior angles]
∠AMC = ∠BMD ...[Vertically opposite angles]
In ΔAMC and ΔBMD,
∠BAC = ∠ABD ...[Proved above]
AM = BM ...[Given]
And ∠AMC = ∠BMD ...[Proved above]
∴ ΔAMC ≅ ΔBMD ...[By ASA congruence rule]
⇒ MC = MD ...[By CPCT]
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if ∠A = 55°, ∠B = 40°, find ∠C.
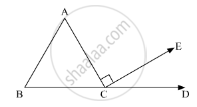
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
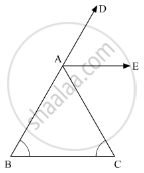
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
If the sides of a triangle are produced in order, then the sum of the three exterior angles so formed is
In the following, find the marked unknown angle:
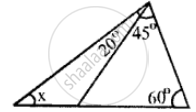
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
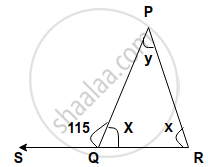
Classify the following triangle according to angle:
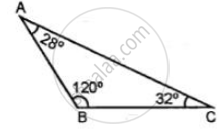
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
17 cm, 7 cm, 8 cm
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
In figure, points lying in the interior of the triangle PQR are ______, that in the exterior are ______ and that on the triangle itself are ______.