Advertisements
Advertisements
प्रश्न
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
उत्तर
Given in the question, bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Now BO is produced to a point M.
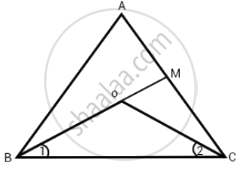
In triangle ABC,
AB = AC
∠ABC = ∠ACB ...[Angle opposite to equal sides of a triangle are equal]
`1/2 ∠ABC = 1/2 ∠ACB`
That is ∠1 = ∠2 ...[Since, BO and CO are bisectors of ∠B and ∠C]
In triangle OBC,
Exterior ∠MOC = ∠1 + ∠2 ...[Exterior angle of a triangle is equal to the sum of interior opposite angles]
Exterior ∠MOC = 2∠1 ...[∠1 = ∠2]
Hence, ∠MOC = ∠ABC.
APPEARS IN
संबंधित प्रश्न
Is the following statement true and false :
An exterior angle of a triangle is less than either of its interior opposite angles.
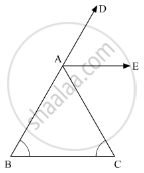
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
State exterior angle theorem.
If two sides of a triangle are 5 cm and 1.5 cm, the length of its third side cannot be ______.
State, if the triangle is possible with the following angles :
20°, 70°, and 90°
Find the value of the angle in the given figure:

Find the unknown marked angles in the given figure:

Can a triangle together have the following angles?
85°, 95° and 22°
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
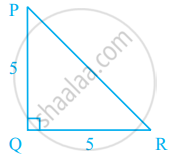
In figure, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆PQR is ______.