Advertisements
Advertisements
Question
Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.
Solution
In triangle PSR, Q is a point on the side SR such that PQ = PR.
To proof that PS > PQ
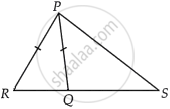
Proof: In triangle PRQ,
PQ = PR ...[Given]
∠R = ∠PQR ...(i) [Angle opposite to equal sides are equal]
∠PQR > ∠S ...(ii) [Exterior angle of a triangle is greater than each of the opposite interior angle]
Now, from equation (i) and (ii), we get
∠R > ∠S
PS > PR ...[Side opposite to greater angle is longer]
PS > PQ ...[PQ = PR]
APPEARS IN
RELATED QUESTIONS
Can a triangle have All angles equal to 60°? Justify your answer in case.
In Δ ABC, BD⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180° − A.
Define a triangle.
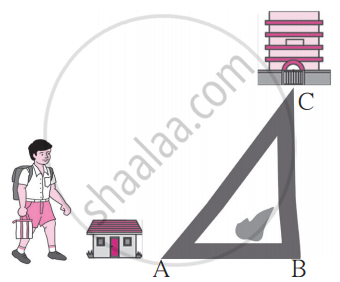
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
The length of the sides of the triangle is given. Say what types of triangles they are 3 cm, 4 cm, 5 cm.
The length of the sides of the triangle is given. Say what types of triangles they are 3.4 cm, 3.4 cm, 5 cm.
The length of the sides of the triangle is given. Say what types of triangles they are 4.3 cm, 4.3 cm, 4.3 cm.
In the given figure, AB is parallel to CD. Then the value of b is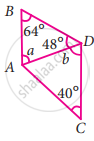
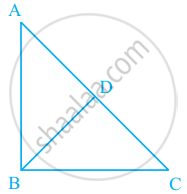
D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
In figure, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is ______.