Advertisements
Advertisements
प्रश्न
Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.
उत्तर
In triangle PSR, Q is a point on the side SR such that PQ = PR.
To proof that PS > PQ
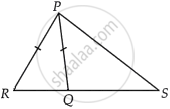
Proof: In triangle PRQ,
PQ = PR ...[Given]
∠R = ∠PQR ...(i) [Angle opposite to equal sides are equal]
∠PQR > ∠S ...(ii) [Exterior angle of a triangle is greater than each of the opposite interior angle]
Now, from equation (i) and (ii), we get
∠R > ∠S
PS > PR ...[Side opposite to greater angle is longer]
PS > PQ ...[PQ = PR]
APPEARS IN
संबंधित प्रश्न
Is the following statement true and false :
Sum of the three angles of a triangle is 180 .
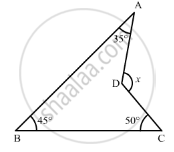
In the given figure, compute the value of x.
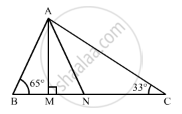
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
In Δ ABC, BD⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180° − A.
If the side BC of ΔABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
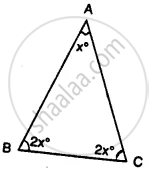
Find the value of the angle in the given figure:
The length of the sides of the triangle is given. Say what types of triangles they are 3 cm, 4 cm, 5 cm.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
7 cm, 24 cm, 25 cm
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
