Advertisements
Advertisements
प्रश्न
Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.
उत्तर
In triangle PSR, Q is a point on the side SR such that PQ = PR.
To proof that PS > PQ
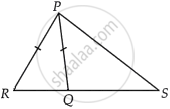
Proof: In triangle PRQ,
PQ = PR ...[Given]
∠R = ∠PQR ...(i) [Angle opposite to equal sides are equal]
∠PQR > ∠S ...(ii) [Exterior angle of a triangle is greater than each of the opposite interior angle]
Now, from equation (i) and (ii), we get
∠R > ∠S
PS > PR ...[Side opposite to greater angle is longer]
PS > PQ ...[PQ = PR]
APPEARS IN
संबंधित प्रश्न
Can a triangle have two right angles? Justify your answer in case.
Is the following statement true and false :
An exterior angle of a triangle is greater than the opposite interior angles.
Fill in the blank to make the following statement true:
A triangles cannot have more than ......obtuse angles.
In ΔABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 120°, then find the measure of ∠A.
In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
Find the unknown marked angles in the given figure:
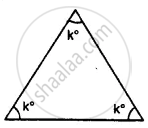
Find, giving a reason, the unknown marked angles, in a triangle drawn below:

Find all the three angles of the ΔABC
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
