Advertisements
Advertisements
प्रश्न
S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.
उत्तर
Given: In ∆PQR, S is any point on side QR.
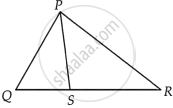
To show: PQ + QR + RP > 2PS
Proof: In ∆PQS,
PQ + QS > PS ...(i) [Sum of two sides of a triangle is greater than the third side]
Similarly, in ∆PRS,
SR + RP > PS ...(ii) [Sum of two sides of a triangle is greater than the third side]
On adding equations (i) and (ii), we get
PQ + QS + SR + RP > 2PS
⇒ PQ + (QS + SR) + RP > 2PS
⇒ PQ + QR + RP > 2PS ...[∵ QR = QS + SR]
APPEARS IN
संबंधित प्रश्न
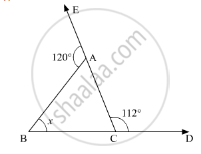
Compute the value of x in the following figure:
Is the following statement true and false :
If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
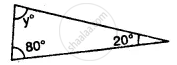
Calculate the unknown marked angles of the following figure :
Classify the following triangle according to sides:
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
Can we have two acute angles whose sum is a right angle? Why or why not?
Which two triangles have ∠B in common?