Advertisements
Advertisements
प्रश्न
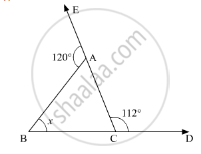
Compute the value of x in the following figure:
उत्तर
In the given problem, we need to find the value of x
In the given ΔABC, ∠ACD = 112° and ∠BAE = 120°
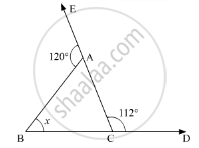
Now, BCD is a straight line. So, using the property, “the angles forming a linear pair are supplementary”, we get,
∠ABC + ∠ACD = 180°
∠ABC + 112 = 180°
∠ACB = 180° - 112°
∠ACB = 68°
Similarly, EAC is a straight line. So, we get,
∠BAE + ∠BAC = 180°
120° + ∠BAC = 180°
∠BAC = 180° - 120°
∠BAC = 60°
Further, using the angle sum property of a triangle,
In ΔABC
∠ACB + ∠BAC + ∠ABC = 180°
68° + 60° + ∠ABC = 180°
128° + ∠ABC = 180° -128°
∠ABC = 52°
Therefore, x = 52°
APPEARS IN
संबंधित प्रश्न
Is the following statement true and false :
A triangle can have at most one obtuse angles.
Is the following statement true and false :
An exterior angle of a triangle is less than either of its interior opposite angles.
If two acute angles of a right triangle are equal, then each acute is equal to
In ΔABC, ∠B = ∠C and ray AX bisects the exterior angle ∠DAC. If ∠DAX = 70°, then ∠ACB =
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Find the value of the angle in the given figure:
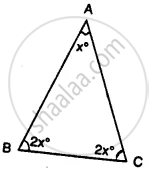
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.