Advertisements
Advertisements
प्रश्न
In ΔABC, ∠B = ∠C and ray AX bisects the exterior angle ∠DAC. If ∠DAX = 70°, then ∠ACB =
विकल्प
35°
90°
70°
55°
उत्तर
In the given ΔABC, ∠B = ∠C . D is the ray extended from point A. AX bisects∠DAC and ∠DAX = 70°
Here, we need to find ∠ACB
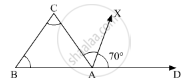
As ray AX bisects ∠DAC
∠CAX = ∠DAX = 70°
Thus,
∠DAC = ∠DAX + ∠XAC
= 70° + 70°
= 140°
Now, according to the property, “exterior angle of a triangle is equal to the sum of two opposite interior angles”, we get,
∠DAC = ∠B + ∠C
140° = 2∠C
`∠C = (140°)/2`
= 70°
Thus, ∠ACB = 70°
APPEARS IN
संबंधित प्रश्न
Is the following statement true and false :
All the angles of a triangle can be less than 60°
Is the following statement true and false :
All the angles of a triangle can be greater than 60°.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
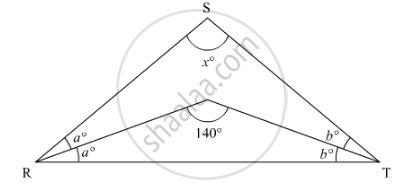
In ΔRST (See figure), what is the value of x?
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
In the following, find the marked unknown angle:

Classify the following triangle according to sides:
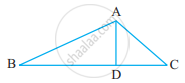
D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
Identify three triangles in the figure.
Which two triangles have ∠B in common?