Advertisements
Advertisements
Question
In ΔABC, ∠B = ∠C and ray AX bisects the exterior angle ∠DAC. If ∠DAX = 70°, then ∠ACB =
Options
35°
90°
70°
55°
Solution
In the given ΔABC, ∠B = ∠C . D is the ray extended from point A. AX bisects∠DAC and ∠DAX = 70°
Here, we need to find ∠ACB
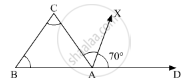
As ray AX bisects ∠DAC
∠CAX = ∠DAX = 70°
Thus,
∠DAC = ∠DAX + ∠XAC
= 70° + 70°
= 140°
Now, according to the property, “exterior angle of a triangle is equal to the sum of two opposite interior angles”, we get,
∠DAC = ∠B + ∠C
140° = 2∠C
`∠C = (140°)/2`
= 70°
Thus, ∠ACB = 70°
APPEARS IN
RELATED QUESTIONS
If the angles of a triangle are in the ratio 1: 2 : 3, determine three angles.
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Can a triangle have two acute angles?Justify your answer in case.
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
If two sides of a triangle are 5 cm and 1.5 cm, the length of its third side cannot be ______.
Classify the following triangle according to sides:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
9 cm, 6 cm, 16 cm
The angles of a triangle are in the ratio 2 : 3 : 4. Then the angles are
In a ∆ABC, AB = AC. The value of x is ________