Advertisements
Advertisements
Question
If the angles of a triangle are in the ratio 1: 2 : 3, determine three angles.
Solution
Given that the angles of a triangle are in the ratio 1: 2 : 3
Let the angles be a, 2a,3a
∴ We know that
Sum of all angles of triangles is `180^@`
`a+2a+3a=180^@`
`6a=180^@`
`a=180^@/6`
`a=30^@`
Since` a=30^@`
`2a=2(30)^@=60^@`
`3a=3(30)^@=90^@`
∴ angles are a =` 30^@,2a=60^@,3a=90^@`
∴ Hence angles are `30^@,60^@ and 90^@`
APPEARS IN
RELATED QUESTIONS
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Is the following statement true and false :
An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
Fill in the blank to make the following statement true:
An exterior angle of a triangle is equal to the two ....... opposite angles.
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
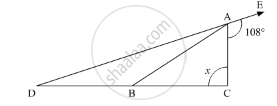
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
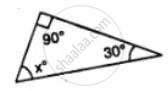
Find the value of the angle in the given figure:
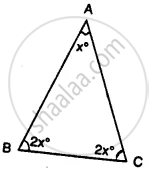
Calculate the unknown marked angles of the following figure :
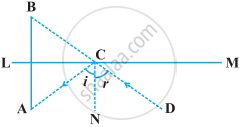
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is point A in its exterior or in its interior?
