Advertisements
Advertisements
Question
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Solution
Given each angle of a triangle less than the sum of the other two
`∴∠A+∠ B+∠C`
`⇒∠A+∠A<∠A+∠B+∠C`
`⇒2∠A<180^@`
[Sum of all angles of a triangle]
`⇒∠A<90^@`
Similarly` ∠ B< 90^@ and ∠C<90^@`
Hence, the triangles acute angled.
APPEARS IN
RELATED QUESTIONS
Is the following statement true and false :
A triangle can have two right angles.
Is the following statement true and false :
All the angles of a triangle can be less than 60°
Fill in the blank to make the following statement true:
A triangle cannot have more than ...... right angles.
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
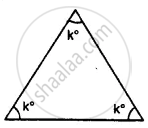
Find the unknown marked angles in the given figure:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
15 cm, 20 cm, 25 cm
Find all the three angles of the ΔABC
S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.
The number of angles in figure is ______.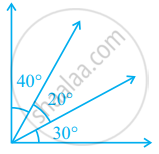
Can we have two acute angles whose sum is a reflex angle? Why or why not?
