Advertisements
Advertisements
Question
S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.
Solution
Given: In ∆PQR, S is any point on side QR.
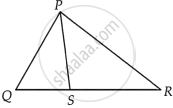
To show: PQ + QR + RP > 2PS
Proof: In ∆PQS,
PQ + QS > PS ...(i) [Sum of two sides of a triangle is greater than the third side]
Similarly, in ∆PRS,
SR + RP > PS ...(ii) [Sum of two sides of a triangle is greater than the third side]
On adding equations (i) and (ii), we get
PQ + QS + SR + RP > 2PS
⇒ PQ + (QS + SR) + RP > 2PS
⇒ PQ + QR + RP > 2PS ...[∵ QR = QS + SR]
APPEARS IN
RELATED QUESTIONS
If the angles of a triangle are in the ratio 1: 2 : 3, determine three angles.
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Is the following statement true and false :
A triangle can have two right angles.
Is the following statement true and false :
An exterior angle of a triangle is greater than the opposite interior angles.
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
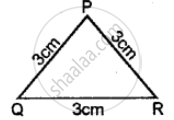
Classify the following triangle according to sides:
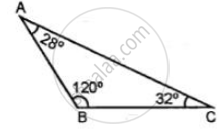
Classify the following triangle according to angle:
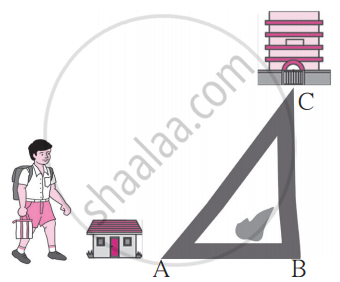
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
The length of the sides of the triangle is given. Say what types of triangles they are 3 cm, 4 cm, 5 cm.
