Advertisements
Advertisements
Question
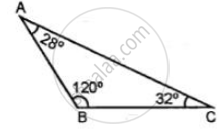
Classify the following triangle according to angle:
Solution
Since, it has an obtuse angle of 120° Hence, it is obtuse-angled triangle.
APPEARS IN
RELATED QUESTIONS
Can a triangle have All angles more than 60°? Justify your answer in case.
Is the following statement true and false :
An exterior angle of a triangle is less than either of its interior opposite angles.
In ΔABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 120°, then find the measure of ∠A.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
In the given figure, show that: ∠a = ∠b + ∠c
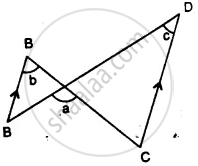
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
Can 30°, 60° and 90° be the angles of a triangle?
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.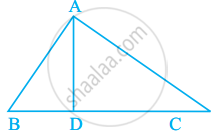
Can we have two acute angles whose sum is a right angle? Why or why not?
Identify three triangles in the figure.