Advertisements
Advertisements
प्रश्न
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
उत्तर
Given in the question, P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q.
To prove: BPQ is an isosceles triangle.
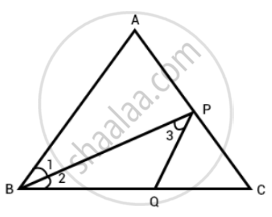
Proof: ∠1 = ∠2 ...(i) [BP is the bisector of ∠ABC]
PQ is parallel to BA and BP cuts them.
So, ∠1 = ∠3 ...[Alternate interior angles as PQ || AB]
∠2 = ∠3 ...[Proved above]
PQ = BQ ...[Sides opposite to equal angle are equal]
Hence, BPQ is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
Can a triangle have two acute angles?Justify your answer in case.
The exterior angles, obtained on producing the base of a triangle both way are 104° and 136°. Find all the angles of the triangle.
Is the following statement true and false :
An exterior angle of a triangle is greater than the opposite interior angles.
Fill in the blank to make the following statement true:
An exterior angle of a triangle is equal to the two ....... opposite angles.
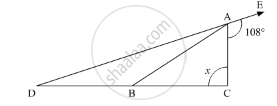
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
Define a triangle.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
Find the value of the angle in the given figure:

The length of the sides of the triangle is given. Say what types of triangles they are 3.4 cm, 3.4 cm, 5 cm.
Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.
