Advertisements
Advertisements
Question
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
Advertisements
Solution
In the given ΔABC,AB = ACand AB is produced to D such that BD = BC
We need to find ∠ACD : ∠ADC
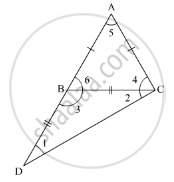
Now, using the property, “angles opposite to equal sides are equal”
As AB = AC
∠6 = ∠4 ........(1)
Similarly,
As BD = BC
∠1 = ∠2 ........(2)
Also, using the property, “an exterior angle of the triangle is equal to the sum of the two opposite interior angle”
In ΔBDC
ext. ∠6 = ∠1 + ∠2
ext. ∠6 = ∠1 + ∠1 (Using 2)
ext. ∠6 = 2∠1
From (1), we get
ext. ∠4 = ∠2 .......(3)
Now, we need to find ∠ACD : ∠ADC
That is,
(∠4 + ∠2): ∠1
(2∠1 + ∠2) : ∠1 (Using 3)
(2∠1 + ∠1) : ∠1(Using 2)
3∠1 :∠1
Eliminating ∠1from both the sides, we get 3:1
Thus, the ratio of ∠ACD :∠ADC is 3 :1
APPEARS IN
RELATED QUESTIONS
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
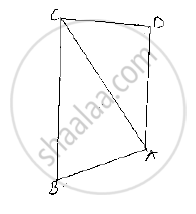
In Fig. 10.131, prove that: (i) CD + DA + AB + BC > 2AC (ii) CD + DA + AB > BC
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
In the given figure, what is the value of x?
In the given figure, if l1 || l2, the value of x is
Which of the following correctly describes the given triangle?
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
In ∆PQR, if ∠R > ∠Q, then ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
