Advertisements
Advertisements
Questions
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Solution
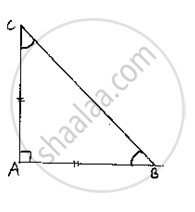
Given to determine the measure of each of the equal angles of right– angled isosceles triangle
Consider on a right – angled isosceles triangle ABC such that
∠A = 90° and AB = AC
Since, AB = AC ⇒ ∠C = ∠B ……….(1)
[Angles opposite to equal sides are equal] Now,
Sum of angles in a triangle = 180°
∠A + ∠B +∠C = 180°
⇒ 90° + ∠B + ∠B = 180° [ ∴∠A = 90° and ∠B = ∠C ]
⇒ 2∠B = 90°
⇒ ∠B = 45°⇒ ∠C = 45°
∴ ∠B =∠C = 45°
Hence, the measure of each of the equal angles of a right-angled isosceles triangle is 45°.
APPEARS IN
RELATED QUESTIONS
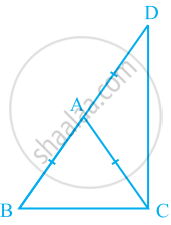
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
Find the measure of each exterior angle of an equilateral triangle.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Which of the following statements are true (T) and which are false (F)?
Difference of any two sides of a triangle is equal to the third side.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
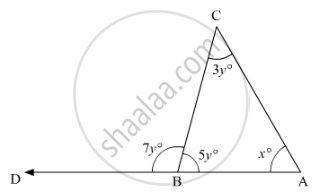
In the given figure, what is the value of x?
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
