Advertisements
Advertisements
Question
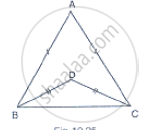
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
Solution
Consider the figure Given
AB = AC, DB = DC and given to find the ratio
∠ABD = ∠ACD
Now,∠ABC and ∠DBC are isosceles triangles since AB = AC and
DB = DC respectively
⇒ ∠ABC = ∠ACB and ∠DBC = ∠DCB [ ∵ angles opposite to equal sides are equal]
Now consider,
∠ABD : ∠ACD
⇒ (∠ABC - ∠DBC ) : (∠ACB - ∠DCB)
⇒ (∠ABC - ∠DBC ) : (∠ABC - ∠DBC ) [∵∠ABC - ∠ACB and ∠DBC = ∠DCB]
⇒ 1:1
∴∠ABD :∠ACD = 1:1
APPEARS IN
RELATED QUESTIONS
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
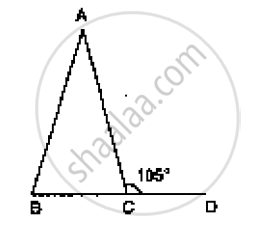
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
Find the measure of each exterior angle of an equilateral triangle.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
The angles of a right angled triangle are
In ∆PQR, if ∠R > ∠Q, then ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
Find all the angles of an equilateral triangle.
