Advertisements
Advertisements
Question
The angles of a right angled triangle are
Options
acute, acute, obtuse
acute, right, right
right, obtuse, acute
acute, acute, right
Solution
The angles of a right angled triangle are acute, acute, right
APPEARS IN
RELATED QUESTIONS
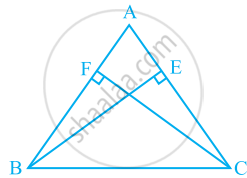
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Fill in the blank to make the following statement true.
In a right triangle the hypotenuse is the .... side.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
In ΔABC, if ∠A = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B =
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
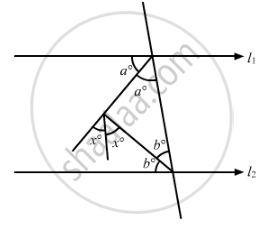
In the given figure, if l1 || l2, the value of x is
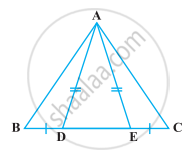
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
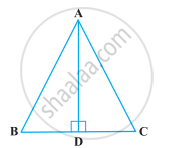
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
