Advertisements
Advertisements
Question
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Advertisements
Solution
Given that ABC is a triangle in which BE and CF are perpendicular to the sides AC and AB respectively such that BE = CF
We have to prove that ΔABC is isosceles
Now, consider ΔBCF and ΔCBE,
We have
∠BFC=CEB=90° [Given]
BC=CB [Common side]
And CF=BE [Given]
So, by RHS congruence criterion, we have ΔBFC≅CEB
Now,
∠FBC=∠EBC [∵ Incongruent triangles corresponding parts are equal]
⇒ ∠ABC=∠ACB
⇒ AC=AB [ ∵Opposite sides to equal angles are equal in a triangle]
∴ ΔABC is isosceles
APPEARS IN
RELATED QUESTIONS
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
Show that the angles of an equilateral triangle are 60° each.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
Which of the following statements are true (T) and which are false (F):
The measure of each angle of an equilateral triangle is 60°
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
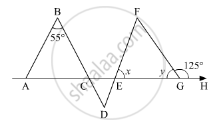
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In the given figure, what is z in terms of x and y?
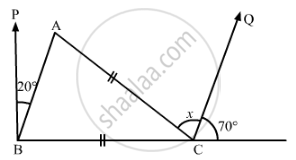
In the given figure, what is y in terms of x?
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
