Advertisements
Advertisements
Question
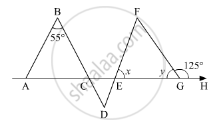
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
Solution
In the given figure,,,and AB ||DE ,BD || FG , ∠FGH =125° and ∠B = 55°
We need to find the value of x and y
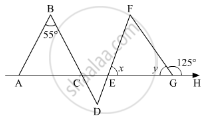
Here, as AB || DE and BD is the transversal, so according to the property, “alternate interior angles are equal”, we get
∠D = ∠B
∠D = 55° ............. (1)
Similarly, as BD || FG and DF is the transversal
∠D = ∠F
∠F = 55° (Using 1)
Further, EGH is a straight line. So, using the property, angles forming a linear pair are supplementary
∠FGE + ∠FGH = 180°
y + 125° = 180°
y = 180° - 125°
y = 55°
Also, using the property, “an exterior angle of a triangle is equal to the sum of the two opposite interior angles”, we get,
In ΔEFG with ∠ FGH as its exterior angle
ext. ∠FGH = ∠F + ∠E
125° = 55° + x
x = 125° - 55°
x = 70°
Thus, x = 70° and y = 55°
APPEARS IN
RELATED QUESTIONS
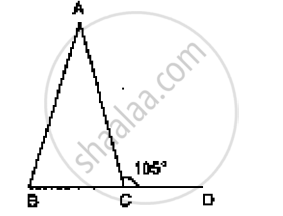
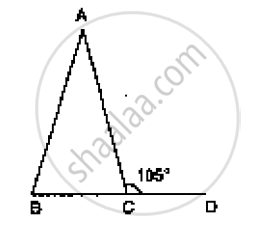
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Fill the blank in the following so that the following statement is true.
In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then

AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
