Advertisements
Advertisements
Question
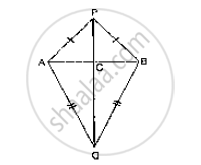
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
Solution
Consider the figure,
We have
AB is a line segment and P,Q are points on opposite sides of AB such that
AP = BP .......(1)
AQ = BQ ........(2)
We have to prove that PQ is perpendicular bisector of AB. Now consider DPAQ and DPBQ,
We have AP = BP [∵ From (1)]
AQ = BQ [∵ From (2)]
And PQ = PQ [Common site]
⇒∠PAQ ≅ ∠PBQ ..….(3) [From SSS congruence]
Now, we can observe that Δ𝐴𝑃𝐵 𝑎𝑛𝑑 Δ𝐴𝐵𝑄 are isosceles triangles.(From 1 and 2)
⟹∠𝑃𝐴𝐵 = ∠𝑃𝐵𝐴 𝑎𝑛𝑑 ∠𝑄𝐴𝐵 = ∠𝑄𝐵𝐴
Now consider ΔPAC and , ΔPBC
C is the point of intersection of AB and PQ.
PA = PB [from (1)]
∠APC = ∠BPC [from (2)]
PC = PC [Common side]
So, from SAS congruency of triangle ΔPAC ≅ ΔPBC
⇒AC = CB and∠PCA = ∠PCB …….(4)
[∵ Corresponding parts of congruent triangles are equal] And also, ACB is line segment
⇒∠ACP + ∠BCP = 180°
But ∠ACP =∠PCB
⇒∠ACP = ∠PCB = 90° ………(5)
We have AC = CB ⇒ C is the midpoint of AB
From (4) and (5)
We can conclude that PC is the perpendicular bisector of AB
Since C is a point on the line PQ, we can say that PQ is the perpendicular bisector of AB.
APPEARS IN
RELATED QUESTIONS
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
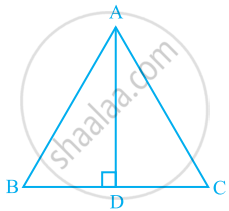
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
In the given figure, what is z in terms of x and y?
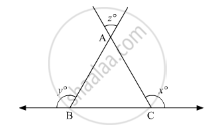
In the given figure, what is the value of x?
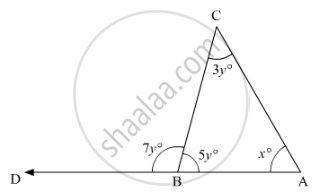
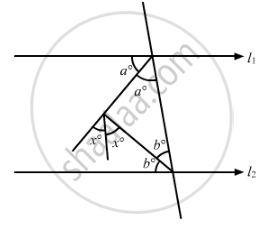
In the given figure, if l1 || l2, the value of x is