Advertisements
Advertisements
Question
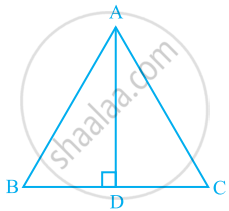
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
Solution
Since AD is the bisector of BC.
∴ BD = CD
Now, in △ABD and △ACD, we have
AD = DA ...[Common]
∠ADB = ∠ADC ...[Each 90°]
BD = CD ...[Proved above]
∴ △ABD ≌ △ACD ...[By SAS congruence]
⇒ AB = AC ...[By Corresponding parts of congruent triangles]
Thus, △ABC is an isosceles triangle.
APPEARS IN
RELATED QUESTIONS
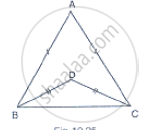
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
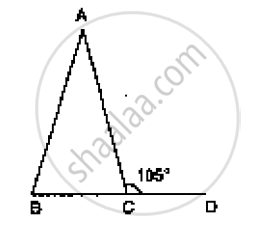
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
Find the measure of each exterior angle of an equilateral triangle.
Fill the blank in the following so that the following statement is true.
Angle opposite to equal sides of a triangle are .....
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
Fill in the blank to make the following statement true.
The sum of any two sides of a triangle is .... than the third side.
In the given figure, what is y in terms of x?

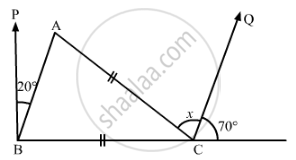
In the given figure, if BP || CQ and AC = BC, then the measure of x is
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
