Advertisements
Advertisements
Question
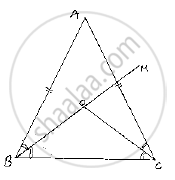
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Solution
Given that in , ΔABC,
AB=AC and the bisector of ∠B and ∠C intersect at O and M is
a point on BO produced
We have to prove ∠ MOC=∠ABC
Since,
AB =AC ⇒ΔABC is isosceles ⇒ ∠B=∠C(or) ∠ABC=∠ACB
Now,
BO and CO are bisectors of ∠ABC and ∠ACB respectively
⇒ABO=∠OBC=∠ACO=∠OB=`1/2` ∠ABC=`1/2`∠ACB ............(1)
We have, in ΔOBC
∠OBC +∠OCB +∠BOC =180° .............(2)
And also
∠BOC +∠COM =180° ..................(3)[Straight angle]
Equating (2) and (3)
⇒ ∠OBC+∠OCB+-∠BOC=∠BOC+∠MOC
⇒ ∠OBC+∠OBC=∠MOC [∵ from (1)]
⇒ 2∠OBBC=∠MOC
⇒2`(1/2∠ABC)`=∠MOC [∵from (1)]
⇒ ∠ABC=∠MOC
∴ ∠MOC=∠ABC
APPEARS IN
RELATED QUESTIONS
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
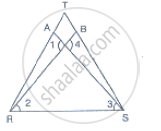
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
Which of the following statements are true (T) and which are false (F)?
Difference of any two sides of a triangle is equal to the third side.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
In the given figure, what is y in terms of x?

In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then

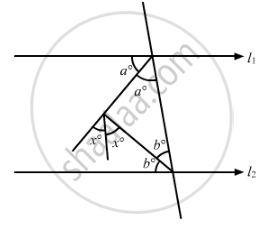
In the given figure, if l1 || l2, the value of x is
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
In ∆PQR, if ∠R > ∠Q, then ______.
Find all the angles of an equilateral triangle.
