Advertisements
Advertisements
प्रश्न
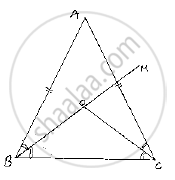
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Advertisements
उत्तर
Given that in , ΔABC,
AB=AC and the bisector of ∠B and ∠C intersect at O and M is
a point on BO produced
We have to prove ∠ MOC=∠ABC
Since,
AB =AC ⇒ΔABC is isosceles ⇒ ∠B=∠C(or) ∠ABC=∠ACB
Now,
BO and CO are bisectors of ∠ABC and ∠ACB respectively
⇒ABO=∠OBC=∠ACO=∠OB=`1/2` ∠ABC=`1/2`∠ACB ............(1)
We have, in ΔOBC
∠OBC +∠OCB +∠BOC =180° .............(2)
And also
∠BOC +∠COM =180° ..................(3)[Straight angle]
Equating (2) and (3)
⇒ ∠OBC+∠OCB+-∠BOC=∠BOC+∠MOC
⇒ ∠OBC+∠OBC=∠MOC [∵ from (1)]
⇒ 2∠OBBC=∠MOC
⇒2`(1/2∠ABC)`=∠MOC [∵from (1)]
⇒ ∠ABC=∠MOC
∴ ∠MOC=∠ABC
APPEARS IN
संबंधित प्रश्न
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
In ∆PQR, if ∠R > ∠Q, then ______.
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
