Advertisements
Advertisements
प्रश्न
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
उत्तर
Given that PQR is a triangle such that PQ = PRand S is any point on the side PQ and ST ||QR.
We have to prove PS = PT
Since, PQ =PR⇒ΔPQR is isosceles
⇒ ∠Q= ∠R(or) ∠PQR= ∠ PRQ
Now,
∠PST=∠PQR and ∠PTS=∠PRQ [Corresponding angles as STllQR ]
Since, ∠PQR=∠PRQ⇒∠PST=∠PTS
Now, In ΔPST,∠PST=∠PTS
⇒ ΔPST is an isosceles triangle
⇒ PS=PT
APPEARS IN
संबंधित प्रश्न
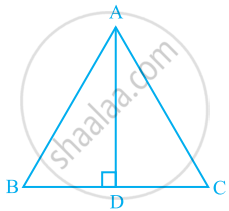
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
