Advertisements
Advertisements
प्रश्न
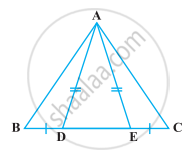
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
उत्तर
In triangle ABD,
AB + BD > AD ...(i)
AC + CD > AD ...(ii) [Sum of the length of any two sides of a triangle must be greater must be greater that the third side]
Adding (i) and (ii), we get
AB + BD + CD + AC > 2AD
AB + BC + CA > 2AD ...[BD = CD as AD is median of triangle ABC]
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

Find the measure of each exterior angle of an equilateral triangle.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
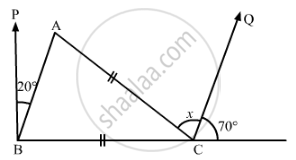
In the given figure, if BP || CQ and AC = BC, then the measure of x is
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
Which of the following correctly describes the given triangle?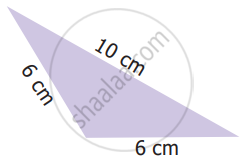
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.