Advertisements
Advertisements
प्रश्न
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
उत्तर
Given that P is a point on the bisector of an angle ABC, and PQ|| AB.
We have to prove that ΔBPQis isosceles
Since,
BP is bisector of ∠ABC⇒∠ABP=∠PBC ............(1)
Now,
PQllAB
⇒ ∠BPQ=∠ABP ................(2)
[alternative angles]
From (1) and (2), we get
∠BPQ=∠PBC(or)∠BPQ=∠PBQ
Now,
In , ΔBPQ
∠BPQ=∠PBQ
⇒ΔBPQ is an isosceles triangle.
∴Hence proved
APPEARS IN
संबंधित प्रश्न
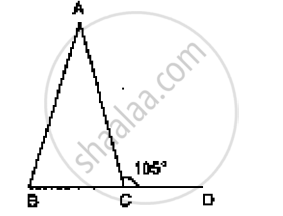
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
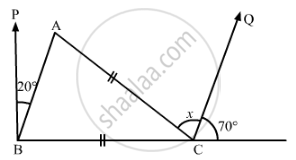
In the given figure, if BP || CQ and AC = BC, then the measure of x is
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
