Advertisements
Advertisements
प्रश्न
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
उत्तर
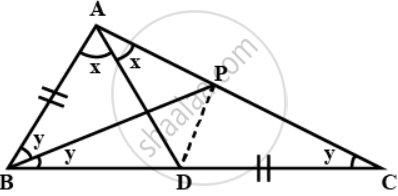
In ΔABC,
∠B = 2∠C or, ∠B = 2y, where ∠C = y.
AD is the bisector of ∠BAC.
So, let ∠BAD = ∠CAD = x.
Let BP be the bisector of ∠ABC. Join PD.
In ΔBPC, we have
∠CBP = ∠BCP = y ⇒ BP = PC
In Δ′s ABP and DCP, we have
∠ABP = ∠DCP,
∠ABP = ∠DCP = y
BP = PC ........(As proved above)
∠ADC = ∠ABD + ∠BAD
⇒ x + 2x = 2y + x
⇒ x = y
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
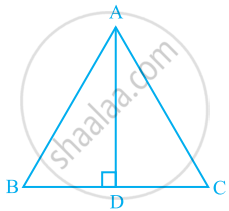
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
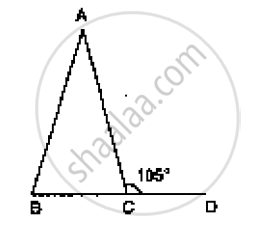
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
In the given figure, x + y =

If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
