Advertisements
Advertisements
प्रश्न
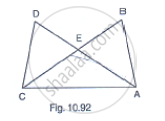
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
उत्तर
Given that in the figure AB =CD and . AD=BC
We have to prove
ΔADC≅ΔCBA
Now,
Consider ΔADC and ΔCBA
We have
AB = CD [Given]
BC = AD [Given]
And AC=AC [Common side]
So, by SSS congruence criterion, we have
ΔADC≅ΔCBA
∴ Hence proved
APPEARS IN
संबंधित प्रश्न
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
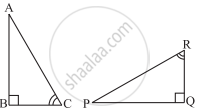
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
