Advertisements
Advertisements
प्रश्न
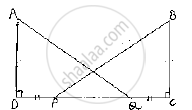
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

उत्तर
Given that, in the figure AD ⊥ CD and CB ⊥ CD and AQ = BP,DP =CQ
We have to prove that ∠DAQ=∠CBP
Given that DP= QC
Add PQ on both sides
Given that DP=QC
Add PQ on both sides
⇒ DP+PQ=PQ+QC
⇒ DQ=PC ................(1)
Now, consider triangle DAQ and CBP,
We have
∠ADQ=∠BCP=90° [given]
AQ=BP [given]
And DQ=PC [given]
So, by RHS congruence criterion, we have ΔDAQ≅ΔCBP
Now,
∠DAQ=∠CBP [ ∵Corresponding parts of congruent triangles are equal]
∴ Hence proved
APPEARS IN
संबंधित प्रश्न
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In the given figure, prove that:
CD + DA + AB + BC > 2AC

Use the information in the given figure to prove:
- AB = FE
- BD = CF

In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
