Advertisements
Advertisements
प्रश्न
In the given figure, prove that:
CD + DA + AB + BC > 2AC

उत्तर
We have to prove that CD + DA + AB + BC > 2AC
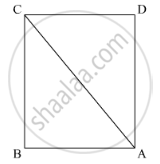
In ΔABC we have
AB + BC > AC (As sum of two sides of triangle is greater than third one) ........(1)
In ΔACDwe have
AD + CD > AC (As sum of two sides of triangle is greater than third one) .........(2)
Hence
Adding (1) & (2) we get AB + BC + AC + CD > 2AC Proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

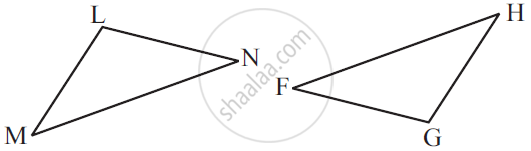
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

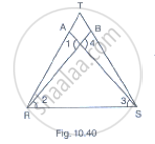
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
