Advertisements
Advertisements
प्रश्न
In the given figure, prove that:
CD + DA + AB > BC
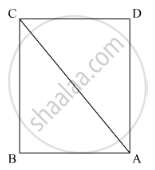
उत्तर
We have to prove that CD + DA + AB > BC
In ΔACD we have
CD + DA > CA (As sum of two sides of triangle is greater than third one)
⇒ CD + DA + AB > CA + AB (Adding AB both sides)
CD + DA + AB > BC Proved.
APPEARS IN
संबंधित प्रश्न
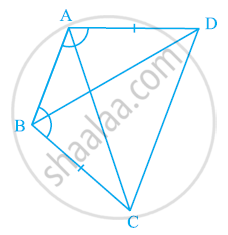
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

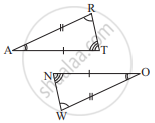
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
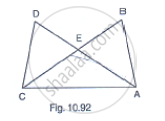
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
