Advertisements
Advertisements
प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

उत्तर
In △BOC and △AOD,
∠OBC = ∠OAD ...[Each 90° (Given)]
∠BOC = ∠AOD ...[Vertically opposite angles]
BC = AD ...[Given]
∴ △BOC ≌ △AOD ...[By AAS congruence rule]
⇒ OB = OA ...[Corresponding parts of congruent triangles]
i.e., O is the mid-point of AB.
So, CD bisects the line segment AB.
APPEARS IN
संबंधित प्रश्न
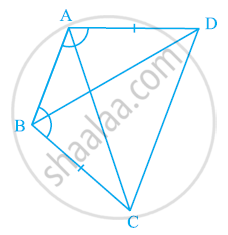
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
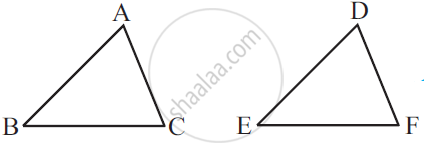
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
Use the information in the given figure to prove:
- AB = FE
- BD = CF

The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
