Advertisements
Advertisements
प्रश्न
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
उत्तर
ABCD is a parallelogram in which ∠A and ∠C are obtuse.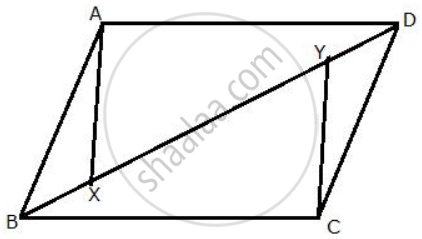
Points X and Y are taken on the diagonal BD.
Such that ∠XAD = ∠YCB = 90°.
We need to prove that XA = YC
Proof:
ln ΔXAD and ΔYCB
∠XAD = ∠YCB= 90° ...[ Given ]
AD = BC ...[ Opposite sides of a parallelogram ]
∠ADX = ∠CBY ...[ Alternate angles ]
∴ By Angle-Side-Angle criterion of congruence,
ΔXAD ≅ ΔYCB
The corresponding parts of the congruent triangles are congruent.
∴ XA = YC ...[ c.p.c.t. ]
Hence proved.
APPEARS IN
संबंधित प्रश्न
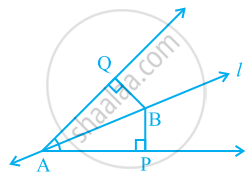
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In the given figure, prove that:
CD + DA + AB + BC > 2AC

In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
