Advertisements
Advertisements
प्रश्न
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
उत्तर
Given: A ΔABQ in which AB is bisected at P
PQ is perpendicular to AB
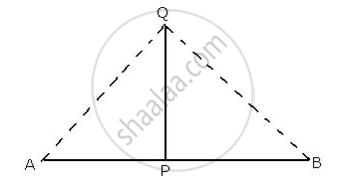
We need to prove that
QA = QB
Proof:
In ΔAPQ and ΔBPQ
AP = PB ...[ P is the mid-point of AB ]
∠QPA = ∠QPB = 90° ...[ PQ is perpendicular to AB ]
PQ = PQ ...[ Common]
∴ By Side-Angel-Side criterion of congruence,
ΔQAP ≅ ΔQBP
The corresponding parts of the congruent triangles are
congruent.
∴ QA = QB ...[ c.p.c.t ]
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

Explain, why ΔABC ≅ ΔFED.
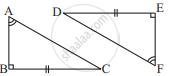
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
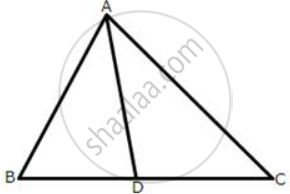
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

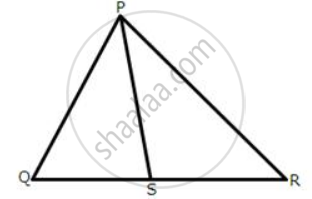
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
