Advertisements
Advertisements
प्रश्न
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
Advertisements
उत्तर
Given: A ΔABC in which D is the mid-point of BC
AD is produced to E so that DE=AD
We need to prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
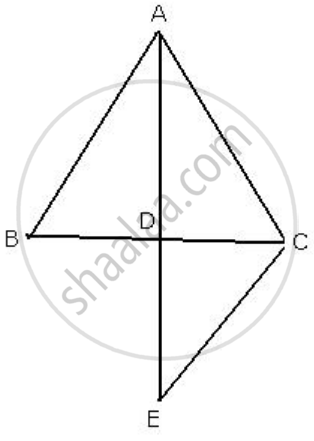
(i) In ΔABD and ΔECD
BD = DC ...[ D is the midpoint of BC ]
∠ADB =∠CDE ...[ vertically opposite angles ]
AD = DE ...[ Given ]
∴ By Side-Angle-Side criterion of congruence, we have,
ΔABD ≅ ΔECD
(ii) The corresponding parts of the congruent triangles are congruent.
∴ AB = EC ...[ c.p.c.t .c]
(iii) Also, ∠BAD = ∠DEC ....[ c.p.c t.c ]
∠ABD = ∠DCE .....[ c.p.c t.c ]
AB || EC .....[ DAB and DEC are alternate angles ]
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =
Explain, why ΔABC ≅ ΔFED.
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
