Advertisements
Chapters
2: Compound Interest (Without using formula)
3: Compound Interest (Using Formula)
4: Expansions (Including Substitution)
5: Factorisation
6: Simultaneous (Linear) Equations (Including Problems)
7: Indices (Exponents)
8: Logarithms
▶ 9: Triangles [Congruency in Triangles]
10: Isosceles Triangles
11: Inequalities
12: Mid-point and Its Converse [ Including Intercept Theorem]
13: Pythagoras Theorem [Proof and Simple Applications with Converse]
14: Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium]
15: Construction of Polygons (Using ruler and compass only)
16: Area Theorems [Proof and Use]
17: Circle
18: Statistics
19: Mean and Median (For Ungrouped Data Only)
20: Area and Perimeter of Plane Figures
21: Solids [Surface Area and Volume of 3-D Solids]
22: Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals]
23: Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios]
24: Solution of Right Triangles [Simple 2-D Problems Involving One Right-angled Triangle]
25: Complementary Angles
26: Co-ordinate Geometry
27: Graphical Solution (Solution of Simultaneous Linear Equations, Graphically)
28: Distance Formula
![Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 9 - Triangles [Congruency in Triangles] Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 9 - Triangles [Congruency in Triangles] - Shaalaa.com](/images/concise-mathematics-english-class-9-icse_6:b313c06da7fb4b0f885a06c3b5e4e4fa.jpg)
Advertisements
Solutions for Chapter 9: Triangles [Congruency in Triangles]
Below listed, you can find solutions for Chapter 9 of CISCE Selina for Concise Mathematics [English] Class 9 ICSE.
Selina solutions for Concise Mathematics [English] Class 9 ICSE 9 Triangles [Congruency in Triangles] Exercise 9 (A) [Pages 122 - 123]
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
If the following pair of the triangle is congruent? state the condition of congruency :
In ΔABC and ΔDEF, ∠B = ∠E = 90o; AC = DF and BC = EF.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
The given figure shows a circle with center O. P is mid-point of chord AB.
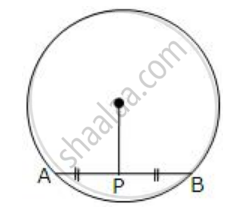
Show that OP is perpendicular to AB.
The following figure shows a circle with center O.
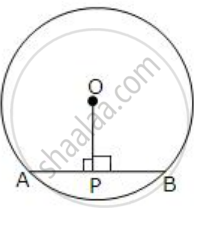
If OP is perpendicular to AB, prove that AP = BP.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC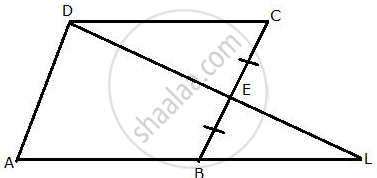
In the given figure, AB = DB and Ac = DC.
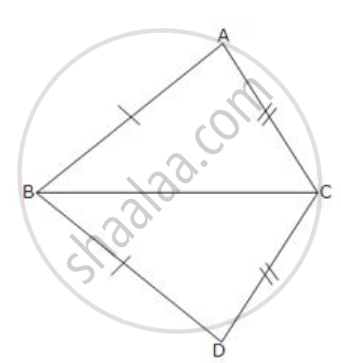
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG
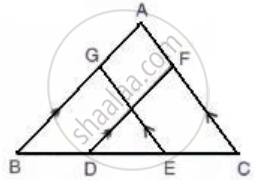
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following figure, BL = CM.
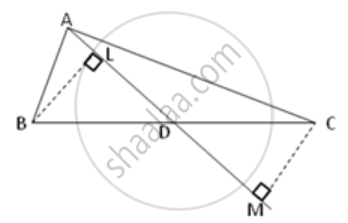
Prove that AD is a median of triangle ABC.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that: BD = CD
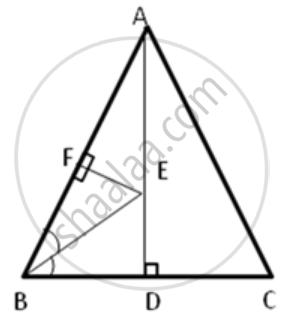
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

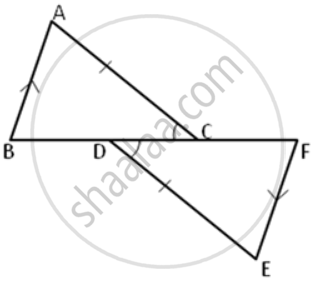
Use the information in the given figure to prove:
- AB = FE
- BD = CF
Selina solutions for Concise Mathematics [English] Class 9 ICSE 9 Triangles [Congruency in Triangles] Exercise 9 (B) [Pages 125 - 126]
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the following diagram, ABCD is a square and APB is an equilateral triangle.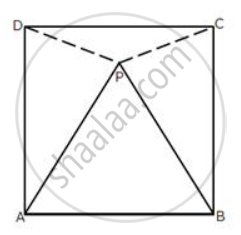
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, ABCD is a square and APB is an equilateral triangle.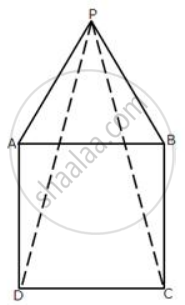
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 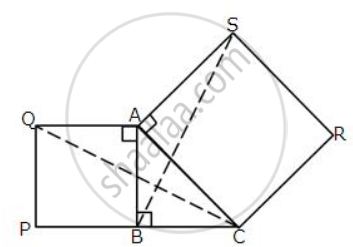
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
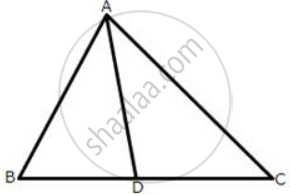
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
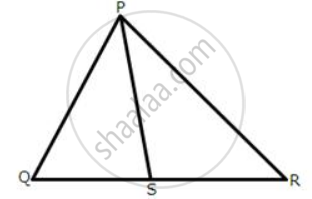 |
In the following diagram, AP and BQ are equal and parallel to each other.
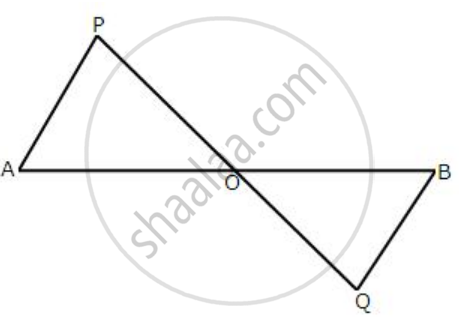
Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB
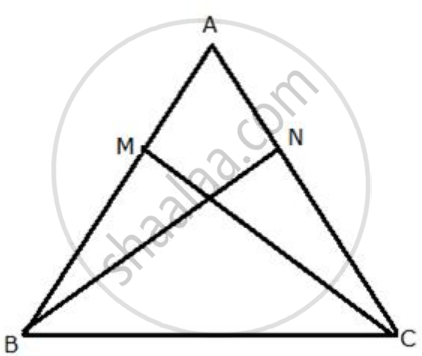
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.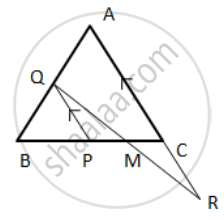
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 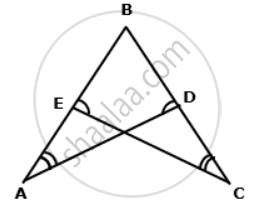
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.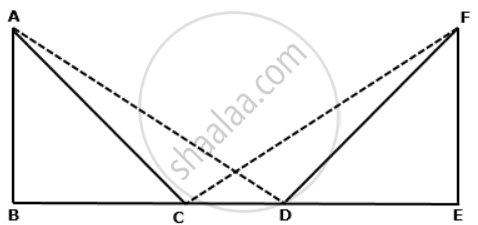
Prove that AD = FC.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
Solutions for 9: Triangles [Congruency in Triangles]
![Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 9 - Triangles [Congruency in Triangles] Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 9 - Triangles [Congruency in Triangles] - Shaalaa.com](/images/concise-mathematics-english-class-9-icse_6:b313c06da7fb4b0f885a06c3b5e4e4fa.jpg)
Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 9 - Triangles [Congruency in Triangles]
Shaalaa.com has the CISCE Mathematics Concise Mathematics [English] Class 9 ICSE CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Selina solutions for Mathematics Concise Mathematics [English] Class 9 ICSE CISCE 9 (Triangles [Congruency in Triangles]) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Concise Mathematics [English] Class 9 ICSE chapter 9 Triangles [Congruency in Triangles] are Relation Between Sides and Angles of Triangle, Important Terms of Triangle, Congruence of Triangles, Criteria for Congruence of Triangles, Concept of Triangles.
Using Selina Concise Mathematics [English] Class 9 ICSE solutions Triangles [Congruency in Triangles] exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Maximum CISCE Concise Mathematics [English] Class 9 ICSE students prefer Selina Textbook Solutions to score more in exams.
Get the free view of Chapter 9, Triangles [Congruency in Triangles] Concise Mathematics [English] Class 9 ICSE additional questions for Mathematics Concise Mathematics [English] Class 9 ICSE CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
