Advertisements
Advertisements
प्रश्न
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

उत्तर
In ΔABC, AB = AC. m and N are points on
AB and AC such that BM = CN
BN and CM are joined

(i) In ΔAMC and ΔANB
AB = AC ...[ Given ] ...(1)
BM = CN ....[ Given ] ...(2)
Subtracting (2) from (1), we have
AB - BM = AC - CN
⇒ AM = AN ...(3)
(ii) Consider the triangles AMC and ANB
AC = AB ...[ given ]
∠AMC = ∠ANB ...[ common 90° ]
AM = AN ....[ from ( 3 ) ]
∴ By the Side-Angel-Side Criterion of congruence, we have ΔAMC ≅ ΔANB
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
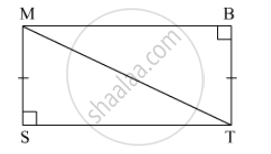
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.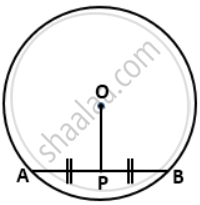
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.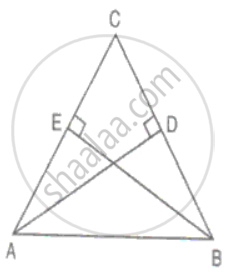
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles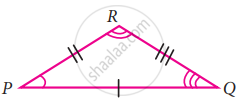
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
