Advertisements
Advertisements
प्रश्न
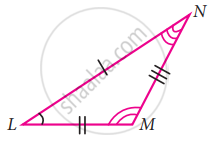
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles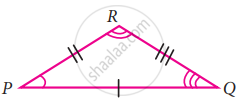
उत्तर
Given: ∆PQR ≅ ∆LNM
(a) Corresponding sides
`bar("PQ") = bar("LN"), bar("PQ") = bar("LM"), bar("RQ") = bar("MN")`
(b) Corresponding angles
∠RPQ = ∠NLM, ∠PQR = ∠LNM, ∠PRQ = ∠LMN
APPEARS IN
संबंधित प्रश्न
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
Mark the correct alternative in each of the following:
If ABC ≅ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
In triangles ABC and PQR three equality relations between some parts are as follows:
AB = QP, ∠B = ∠P and BC = PR
State which of the congruence conditions applies:
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
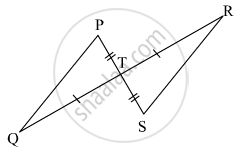
From the information shown in the figure,
in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...[Vertically opposite angles]
∴ ΔPTQ ≅ ΔSTR ...`square` test
∴ `{:("∠TPQ" ≅ square),("and" square ≅ "∠TRS"):}}` ...corresponding angles of congruent triangles
seg PQ ≅ `square` ...corresponding sides of congruent triangles
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

State, whether the pairs of triangles given in the following figures are congruent or not:

In the given figure, prove that: ∆ ABD ≅ ∆ ACD
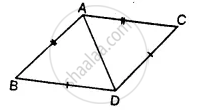
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
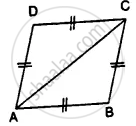
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.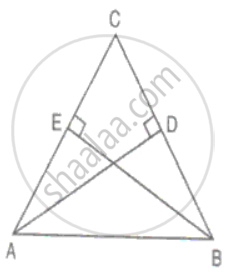
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
