Advertisements
Advertisements
प्रश्न
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
उत्तर
Given:
In the figure, OA=OC, AB =BC
We need to prove that,
AOB = 90°
(i) In ΔABO and ΔCBO,
AB = BC ...[given ]
AO = CO ...[ given ]
OB = OB ...[ common ]
∴By Side-Side-Side criterion of congruence, we have
ΔABO ≅ ΔCBO
The corresponding parts of the congruent triangles are congruent.
∴∠ABO = ∠CBO ...[c. p.c.t. ]
⇒ ∠ABD = ∠CBD
and ∠AOB = ∠COB ...[c. p.c t ]
We have
∠AOB + ∠COB = 180° .....[ linear pair ]
⇒ ∠AOB = ∠ COB= 90° and AC ⊥ BD
(ii) In ΔAOD and ΔCOD,
OD = OD ...[ common ]
∠AOD = ∠COD ...[ each=90° ]
AO = CO ...[ given]
∴By Side-Angel-Side criterion of congruence, we have
ΔAOD ≅ ΔCOD
(iii) The corresponding parts of the congruent
triangles are congruent.
∴AD = CD ...[c. p.c t ]
Hence proved.
APPEARS IN
संबंधित प्रश्न
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
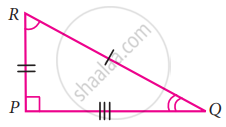
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
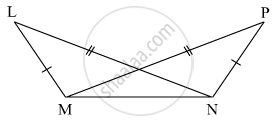
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
State, whether the pairs of triangles given in the following figures are congruent or not:

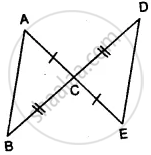
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.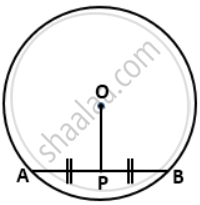
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.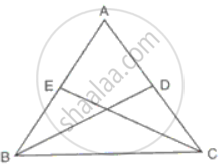
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles