Advertisements
Advertisements
प्रश्न
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

उत्तर
In ΔABC, AB = AC. m and N are points on
AB and AC such that BM = CN
BN and CM are joined

(i) The corresponding parts of the congruent triangles are congruent.
∴ CM = BN ....[ c.p.c.t ] ...(1)
(ii) Consider the triangles ΔBMC and ΔCNB
BM = CN ...[ given ]
BC = BC ...[ common ]
Cm = BN ..[ from (1) ]
∴ By Side-Side-Side criterion of congruence, we have ΔBMC ≅ ΔCNB
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠E
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
State, whether the pairs of triangles given in the following figures are congruent or not:
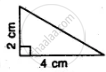

State, whether the pairs of triangles given in the following figures are congruent or not:
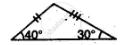
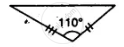
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.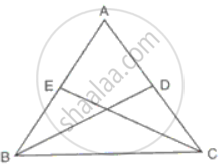
In the given figure, AB = DB and AC = DC. Find the values of x and y.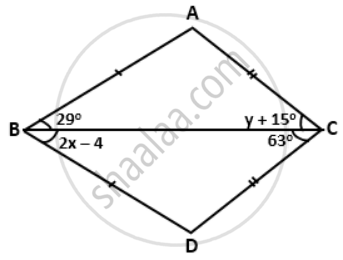
Two figures are congruent, if they have the same shape.
