Advertisements
Advertisements
Question
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

Solution
In ΔABC, AB = AC. m and N are points on
AB and AC such that BM = CN
BN and CM are joined

(i) The corresponding parts of the congruent triangles are congruent.
∴ CM = BN ....[ c.p.c.t ] ...(1)
(ii) Consider the triangles ΔBMC and ΔCNB
BM = CN ...[ given ]
BC = BC ...[ common ]
Cm = BN ..[ from (1) ]
∴ By Side-Side-Side criterion of congruence, we have ΔBMC ≅ ΔCNB
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(EF)`
Complete the congruence statement:
ΔBCA ≅?
ΔQRS ≅?
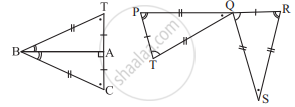
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
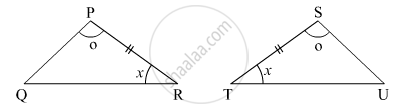
By ______ test
ΔPRQ ≅ ΔSTU
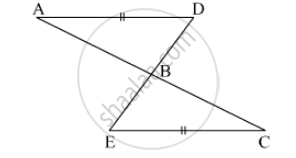
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.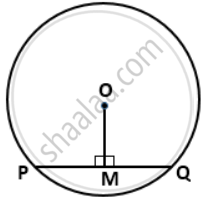
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.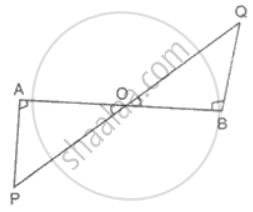
If AB = QR, BC = PR and CA = PQ, then ______.
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
