Advertisements
Advertisements
Question
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
Solution
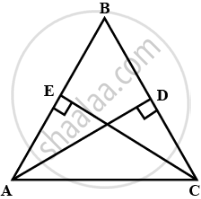
ln ΔABD and ΔCBE,
AB = BC ....(given)
AD ⊥ BC
CE ⊥ AB
To proved:
In ΔABD & ΔCBE
∠ ADB = ∠ CEB = 90° ....[Perpendiculars]
∠B = ∠B ....(Common angle)
AB = BC
∴ ΔABD ≅ ΔCBE ....(by AAS congruence)
⇒ AD = CE ...(c.p.c.t.c)
APPEARS IN
RELATED QUESTIONS
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

In the given figure, prove that:
CD + DA + AB + BC > 2AC

The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
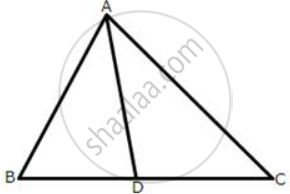
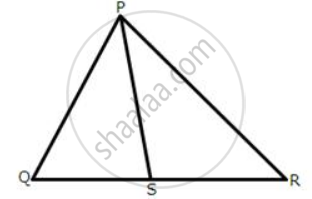
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
