Advertisements
Advertisements
Question
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
Solution
Given: A(ΔABC) in which BD is the median to AC.
BD is produced to E such that BD = DE,
We need to prove that AE II BC.
Construction: Join AE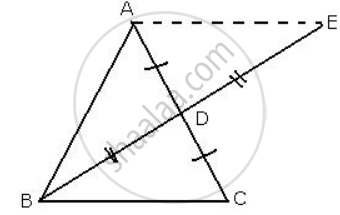
Proof:
AD = DC ...[ BD is median to AC ] ...(1)
In ΔBDC and ΔADE,
BD = DE ...[ Given ]
∠BDC = ∠ADE = 90° ...[ Vertically opposite angles ]
AD = DC ...[ from(1) ]
∴ By Side-Angle-Side Criterion of congruence,
ΔBDC ≅ ΔADE
The corresponding parts of the congruent triangles are congruent.
∴ ∠EAD = ∠BCD ...[ c.p.c.t. ]
But these are alternate angles and AC is the transversal.
Thus, AE || BC.
APPEARS IN
RELATED QUESTIONS
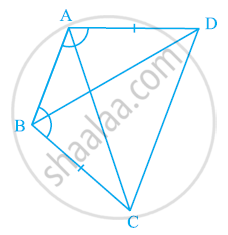
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
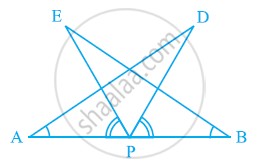
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
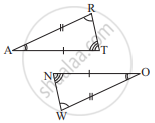
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
