Advertisements
Advertisements
Question
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
Solution
Given: A( ΔPQR ) in which QX is the bisector of ∠Q. and RX is the bisector of ∠R.
XS ⊥ QR and XT ⊥ PQ.
We need to prove that
(i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
Construction: Draw XZ ⊥ PR and join PX.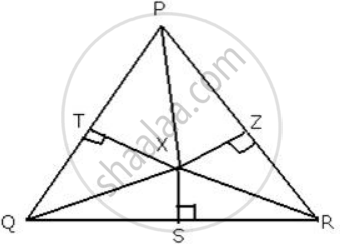
Proof:
(i) In ΔXTQ and ΔXSQ,
∠QTX = ∠QSX = 90° ...[ XS ⊥ QR and XT ⊥ PQ ]
∠TQX = ∠SQX ...[ QX is bisector of ∠Q ]
QX = QX ...[ Common ]
∴ By Angle-Side-Angle Criterion of congruence,
ΔXTQ ≅ ΔXSQ
(ii) The corresponding parts of the congruent triangles are congruent.
∴ XT = XS ...[ c.p.c.t. ]
In ΔXSR & ΔXRZ
∠XSR = ∠XZR = 90° ...[ XS ⊥ QR and ∠XSR = 90° ]
∠XRS = ∠ZRX ...[ RX is bisector of ∠R ]
RX = RX ....[ Common ]
∴ By Angle-Angle-Side criterion of congruence,
ΔXSR ≅ ΔXRZ
The corresponding parts of the congruent triangles are congruent.
∴ XS = XT ...[ c.p.c.t. ]
From (1) and (2)
XT = XZ
In ΔXTP and ΔPZX
∠XTP = ∠XZP = 90° ....[ Given ]
XP = XP ....[ Common ]
XT = XZ
∴ By Right angle-Hypotenuse-side criterion of congruence,
ΔXTP ≅ ΔPZX
The corresponding parts of the congruent triangles are
congruent.
∴ ∠TPX = ∠ZPX ...[ c.p.c.t. ]
∴ PX bisects ∠P.
APPEARS IN
RELATED QUESTIONS
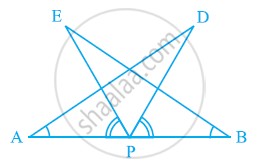
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

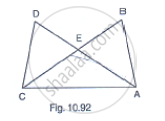
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
