Advertisements
Advertisements
Question
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
Solution
Given: in the figure, O is center of the circle, and AB is chord. P is a point on AB such that AP = PB.
We need to prove that, OP ⊥ AB
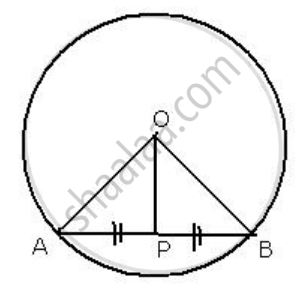
Construction: Join OA and OB
Proof:
In ΔOAP and ΔOBP
OA = OB ...[radii of the same circle]
OP = OP ...[common]
AP = PB ...[given]
∴ By Side-Side-Side criterion of congruency,
ΔOAP ≅ ΔOBP
The corresponding parts of the congruent triangles are congruent.
∴ ∠OPA = ∠OPB ...[by c.p.c.t]
But ∠OPA + ∠OPB = 180° ...[linear pair]
∴ ∠OPA = ∠OPB = 90°
Hence OP ⊥ AB.
APPEARS IN
RELATED QUESTIONS
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

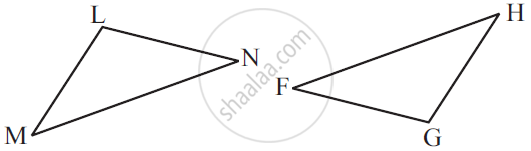
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the given figure, AB = DB and Ac = DC.
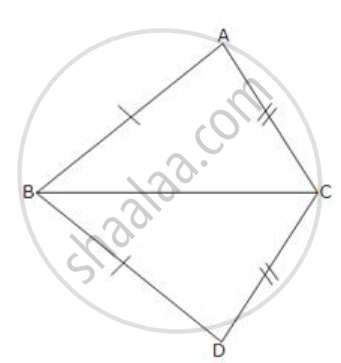
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
