Advertisements
Advertisements
Question
In the given figure, AB = DB and Ac = DC.
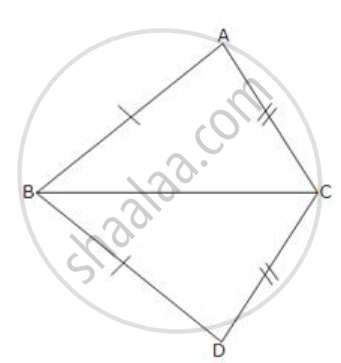
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
Solution
Given:
In the figure AB = DB, AC = DC, ∠ABD = 58°,
∠DBC = ( 2x - 4 )°, ∠ACB = ( y +15)° and ∠DCB = 63°
We need to find the values of x and y.
In ΔABC and ΔDBC
AB = DB ...[ Given ]
AC= DC ...[ Given ]
BC= BC ...[ common ]
∴ By Side-SIde-Side criterion of congruence, we have,
ΔABC ≅ ΔDBC
The corresponding parts of the congruent triangles are congruent.
∴ ∠ABC= DCB ...[ c. p. c .t ]
⇒ y° + 15° = 63°
⇒ y° = 63° - 15°
⇒ y° = 48°
and ∠ABC =∠DBC ...[ c.p.c.t ]
But, ∠DBC = ( 2x - 4)°
We have ∠ABC + ∠DBC = ∠ABD
⇒ (2x - 4)° + (2x - 4)° = 58°
⇒ 4x - 8°= 58°
⇒ 4x = 58° + 8°
⇒ 4x = 66°
⇒ X = ` 66°/(4)`
⇒ X = 16.5°
Thus the values of x and y are :
x = 16.5° and y = 48°
APPEARS IN
RELATED QUESTIONS
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
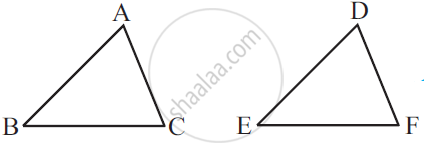
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
