Advertisements
Advertisements
Question
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
Solution
Given: A ΔABC in which ∠B = ∠C.
DL is the perpendicular from D to AB
DM is the perpendicular from D to AC
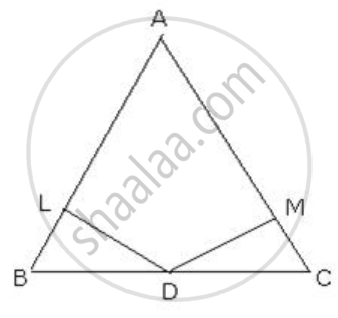
We need to prove that
DL = DM
Proof:
In ΔDLB and ΔDMC
∠DLB = ∠DMC=900 ...[ DL ⊥ AB and DM ⊥ AC ]
∠B=∠C ...[ Given ]
BD= DC ...[ D is the midpoint of BC ]
∴ By Angel-Angel-SIde Criterion of congruence,
ΔDLB ≅ ΔDMC
The corresponding parts of the congruent triangles are congruent.
∴DL=DM ...[ c.p.c.t ]
APPEARS IN
RELATED QUESTIONS
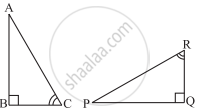
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
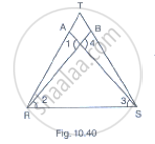
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
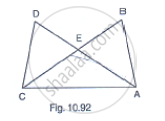
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
