Advertisements
Advertisements
Question
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
Solution
Given: A ΔABC in which AD is the perpendicular bisector of BC
BE is the perpendicular bisector of CA
CF is the perpendicular bisector of AB
AD, BE and CF meet at I

WE need to prove that
IA = IB= IC
Proof:
In ΔBID and ΔCID
BD = DC ...[ Given ]
∠BDI = ∠CDI = 90°...[ AD is the perpendicular bisector of BC]
DI = DI ...[ Common ]
∴ By the Side-Angle-Side criterion of congruence,
Δ BID ≅ Δ CID
The corresponding parts of the congruent triangles are congruent.
∴ IB = IC ...[ c.p.c.t ]
Similarly, in Δ CIE and Δ AIE
CE = AE ...[ Given ]
∠CEI = ∠AEI = 90° ...[ AD is the perpendicular bisector of BC ]
IE = IE ...[ Common ]
∴ By Side-Angel-Side Criterion of congruence,
ΔCIE ≅ ΔAIE
The corresponding parts of the congruent triangles are congruent.
∴ IC = IA ...[ c.p.c.t ]
Thus, IA = IB = IC
APPEARS IN
RELATED QUESTIONS
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
In the given figure, AB = DB and Ac = DC.
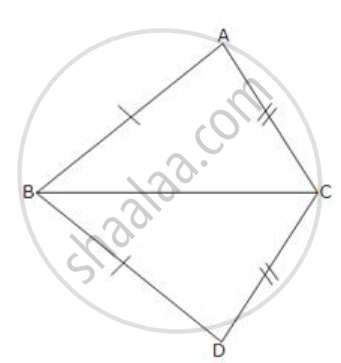
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
