Advertisements
Advertisements
Question
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
Solution
It is given that ∠A = ∠D , ∠B = ∠E , ∠C = ∠F
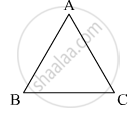
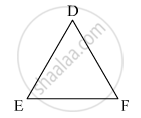
For necessarily triangle to be congruent, sides should also be equal.
APPEARS IN
RELATED QUESTIONS
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
In the given figure, AB = DB and Ac = DC.
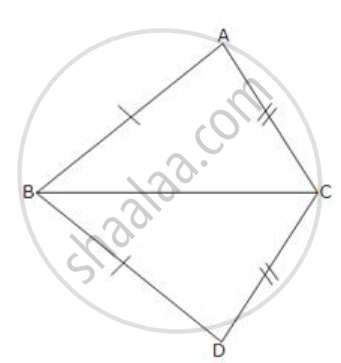
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
